[ed. note: poker research was something I started a while back with my friend Pat Wong when we were developing pokerbots. The ideas in this are from those conversations – thanks Pat!]
When playing holdem, the key strategic tension is the need to play as many hands as possible, versus the need to only play “good” hands. Thanks to the mandatory antes when in the small and big blind positions, one cannot simply fold until you get pocket Aces (AA). There are only 6 possible draws of AA out of 1326 possible 2-card draws. As it turns out, you win about 80% of the time with AA, but you are only playing 6/1326 = 0.45% of the time. Meanwhile, at a table with 10 players, 2/10 times you have a mandatory ante as big or small blind, which is a much more steady drain on your capital.
There are lots of books written on opening strategy, but I was interested to see if there was an expectation based approach to playing as many hands as is reasonable to see the flop without having a negative expectation value.
To do so, we must first figure out the probabilities. As discussed in my previous post, you can figure out a decent estimate of the winning percentages of each two hand combination. There are 1326 possible two handed cards that can be drawn from a 52 card deck, but you can simplify this by only considering whether the cards are suited (s) or off-suit (d); this drops the number of combinations to 169.
Next, we have to take into account the effect of playing against multiple players. I did a brute force calculation showing the win/loss/tie percentages against 2 or 3 players (ie. you against one opponent or two opponents). Usually you can simplify matters by simply assuming that each opponent is an independent game – but I wanted to do the research to see how close this is to the truth.
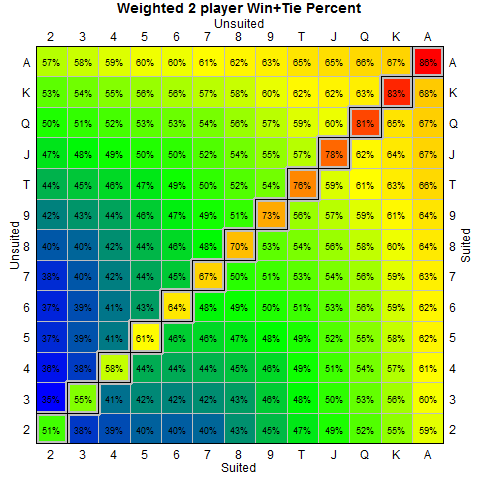
Above is a hand table showing the percentage chance of winning for 2 and 3 players. Obviously the odds of winning drops the more opponents you face, but what keeps the game interesting is that the pot increases faster than the odds drop. Note that these are the unweighted probabilities – i.e. it doesn’t take into account the fact that no sane opponent is going to play 27d. Now if you are facing a big blind that hasn’t put up any money beyond their ante – so no raises thus far – then the unweighted probability table is the one you would use. On the other hand, if you want to consider the “real” tables where players would fold crappier cards (a process discussed in my earlier post) then you would want the weighted probability tables – in general I’ll use these weighted numbers going forward.
To see the effect of my weighting, here’s a quick graph showing the unweighted versus weighted probabilities. Note that my weighting schedule is certainly open to criticism – you may have a very different estimate as to how to do the weighting of opponents.
I wanted to see how closely I could estimate for multiple players. If a 3 player game were equivalent to 2 independent games played at the same time, then you would see the probability of winning be the square of the 2 player game. Let’s say you have cards with a 50% chance of winning against a single opponent. For an independent game, that means the chance of winning should drop to 25% (i.e. 50% x 50%). However, in texas holdem, you have shared community cards so they are clearly not independent. The question is by how much they are not independent. Below is a graph showing how much of a differential there is between the independent case (i.e. just squaring the 2 player probability) versus what we see when we do an exhaustive calculation.
The graph shows that this actually underestimates your change of winning. If your hole cards are good enough to beat one player, then you are more likely to beat the second player. This adds about 8% to your chance of winning versus the calculation assuming independence (that’s what the histogram below is showing). These are unweighted estimates by the way. For the rest of the calculations I’ll be using the actual odds, not just an estimate – mainly because it took 4 solid days of computer time to calculate them, so why throw them away? I’m curious about how 4-10 players would look but I fear the calculation time that would take – I’m not willing to blow the money on EC2 to figure out a hunch.
Okay – here’s where the rubber hits the road. We have our weighted probabilities for 3 players. We can now figure out which cards we should play to minimize the cost of seeing the flop. We need one additional set of assumptions. I’m assuming a 10 person table, but that most of the time people fold so that there are only 3 opponents willing to see the flop. Therefore, the expected value of folding is (on average) equal to the cost of the ante for the big and small blinds. Assuming ante is $1, that means if you did nothing but fold and never played a hand, your average cost per fold is $1/10 + $0.5/10 (the ante’s for the blinds averaged over the 10 players). But we will be playing some hands – let’s assume for simplicity sake that the cost of losing is $1 (the cost of your ante assuming no raises). On the other hand, the profit from winning is $2.5 (i.e. you get the ante’s from the two opponents, plus the small blind assuming they fold as well).
This gives us a way of calculating the expectation value for our strategy. If we play 50% of the hands, and the hands we do play have a 40% chance of winning, then the expectation is:
Expected Value = 50% x (-$1.5/10) + 50% x (40% x $2.5 – 60% x $1) = $0.55
Now, let’s look at the weighted win percentages for the cards from above. If we set a cutoff percentage where we play cards with greater than the cutoff and fold cards with win probabilities below the cutoff – and we calculate a weighted expectation given the win percentages for each card pair, then we can create a quick graph that shows us the cutoff with the maximum expectation:
Going back to our weighted win percentages, that gives us the following table:
The values in pink (red is too hard to read) show us the cards that we play. The values in blue are the ones we fold. Yellow values are ones on the line (i.e. within 10% of the cutoff value). If we play these cards, we’ll see enough flops and have a good enough chance of winning to be basically breakeven. At this point, your skill at playing poker and bluffing has to come in – which is where you’ll see your profits.
As an exercise, I simulated playing 1,000,000 hands to see what your bank balance would look like under this strategy – on average its about breakeven (showing a profit of $6000 over 1 million hands is about $0.006/hand). The bottom histogram also looks at drawdowns – i.e. once you hit a new high, how far down will you go on average. Again, given it is 1 million hands, there’s not too much variance in there.
I’m trying to build this into a nice spreadsheet that you can use to create your own strategies – I did most of this work in R and it’s not easy to go from code to spreadsheets. I’ll post an update when I figure it out.